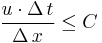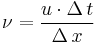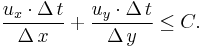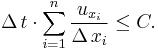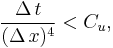Courant–Friedrichs–Lewy condition
In mathematics, the Courant–Friedrichs–Lewy condition (CFL condition) is a necessary condition for convergence while solving certain partial differential equations (usually hyperbolic PDEs) numerically by the method of finite differences.[1] It arises when explicit time-marching schemes are used for the numerical solution. As a consequence, the time step must be less than a certain time in many explicit time-marching computer simulations, otherwise the simulation will produce wildly incorrect results. The condition is named after Richard Courant, Kurt Friedrichs, and Hans Lewy who described it in their 1928 paper.[2]
Contents |
Heuristic description
The information behind the condition is that, for example, if a wave is moving across a discrete spatial grid and we want to compute its amplitude at discrete time steps of equal length,[3] then this length must be less than the time for the wave to travel adjacent grid points. As a corollary, when the grid point separation is reduced, the upper limit for the time step also decreases. In essence, the numerical domain of dependence of any point in space and time (which data values in the initial conditions affect the numerical computed value at that point) must include the analytical domain of dependence (where in the initial conditions has an effect on the exact value of the solution at that point) in order to assure that the scheme can access the information required to form the solution.
The CFL condition
In order to make a reasonably formally precise statement of the condition, it is necessary to define the following quantities
- Spatial coordinate: it is one of the coordinates of the physical space in which the problem is posed.
- Spatial dimension of the problem: it is the number
 of spatial dimensions i.e. the number of spatial coordinates of the physical space where the problem is posed. Typical values are
of spatial dimensions i.e. the number of spatial coordinates of the physical space where the problem is posed. Typical values are 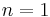 ,
, 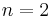 and
and 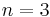 .
. - Time: it is the coordinate, acting as a parameter, which describes the evolution of the system, distinct from the spatial coordinates.
The spatial coordinates and the time are supposed to be discrete valued independent variables, whose minimal steps are called respectively the interval length[4] and the time step: the CFL condition relates the length of the time step to a function interval lengths of each spatial variable.
Operatively, the CFL condition is commonly prescribed for those terms of the finite-difference approximation of general partial differential equations which model the advection phenomenon.[5]
The one–dimensional case
For one-dimensional case, the CFL has the following form:
where
 is the velocity (whose dimension is Length/Time)
is the velocity (whose dimension is Length/Time)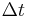 is the time step (whose dimension is Time)
is the time step (whose dimension is Time)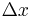 is the length interval (whose dimension is Length),
is the length interval (whose dimension is Length), is a dimensionless constant which depends only on the particular equation to be solved.[6]
is a dimensionless constant which depends only on the particular equation to be solved.[6]
is called the Courant number.
The two and general n–dimensional case
In the two–dimensional case, the CFL condition becomes
with obvious meaning of the symbols involved. In analogy with the two–dimensional case, the general CFL condition for the  –dimensional case is the following one
–dimensional case is the following one
Note that the interval length it is not required to be the same for each spatial variable 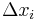 ,
,  = 1 ,...,
= 1 ,...,  . This "degree of freedom" can be used in order to somewhat optimize the value of the time step for a particular problem, by varying the values of the different interval in order to keep it not too small.
. This "degree of freedom" can be used in order to somewhat optimize the value of the time step for a particular problem, by varying the values of the different interval in order to keep it not too small.
Implications of the CFL condition
The CFL condition is only a necessary one
As already remarked, the CFL condition is a necessary condition, but may not be sufficient for the convergence of the Finite-difference approximation of a given numerical problem. Thus, in order to establish the convergence of the finite-difference approximation, it is necessary to use other methods, which in turn could imply further limitations on the length of the time step and/or the lengths of the spatial intervals.
The CFL condition can be a very strong requirement
The CFL condition can be a very limiting constraint on the time step 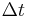 : for example, in the finite-difference approximation of certain fourth-order nonlinear partial differential equations, it can have the following form
: for example, in the finite-difference approximation of certain fourth-order nonlinear partial differential equations, it can have the following form
meaning that a decrease in the length interval 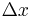 requires a fourth order decrease in the time step
requires a fourth order decrease in the time step 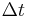 for the condition to be fulfilled. Therefore, when solving particularly stiff problems, efforts are often made to avoid the CFL condition, for example by using implicit methods. However, in a recent work,[7] a modern dynamical systems approaches to modeling, based upon center manifold theory, is demonstrated to provide theoretical support for the construction of non-traditional discretisations that automatically overcome the CFL restriction: see the article by Roberts (2003) for further information.
for the condition to be fulfilled. Therefore, when solving particularly stiff problems, efforts are often made to avoid the CFL condition, for example by using implicit methods. However, in a recent work,[7] a modern dynamical systems approaches to modeling, based upon center manifold theory, is demonstrated to provide theoretical support for the construction of non-traditional discretisations that automatically overcome the CFL restriction: see the article by Roberts (2003) for further information.
See also
- Richard Courant
- Finite difference method
- Kurt Otto Friedrichs
- Implicit method
- Hans Lewy
- Numerical analysis
Notes
- ^ In general, it is not a sufficient condition: also, it can be also a demanding condition for some problems. See the "Implications of the CFL condition" section of this article for a brief survey of this issues.
- ^ See reference Courant, Friedrichs & Lewy 1928. There exists also an English translation of the 1928 German original: see references Courant, Friedrichs & Lewy 1956 and Courant, Friedrichs & Lewy 1967.
- ^ This situation commonly occurs when a hyperbolic partial differential operator has been approximated by a finite difference equation, which is then solved by numerical linear algebra methods.
- ^ This quantity is not necessarily the same for for each spatial variable, as it is shown in the "[[Courant–Friedrichs–Lewy condition#The two and general n–dimensional case|The two and general n–dimensional case]]" section of this entry : it can be chosen in order to somewhat relax the condition.
- ^ Precisely, this is the hyperbolic part of the PDE under analysis.
- ^ Precisely, it does not depend on the time step
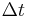 and on the length interval
and on the length interval 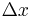 .
. - ^ See section 3 in the article by Roberts (2003)
References
- Courant, R.; Friedrichs, K.; Lewy, H. (1928), "Über die partiellen Differenzengleichungen der mathematischen Physik" (in German), Mathematische Annalen 100 (1): 32–74, Bibcode 1928MatAn.100...32C, doi:10.1007/BF01448839, JFM 54.0486.01, MR1512478, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002272636.
- Courant, R.; Friedrichs, K.; Lewy, H. (September 1956) [1928], On the partial difference equations of mathematical physics, AEC Researh and Development Report, NYO-7689, New York: AEC Computing and Applied Mathematics Centre – Courant Institute of Mathematical Sciences, pp. V + 76, archived from the original on October 23, 2008, http://www.archive.org/stream/onpartialdiffere00cour#page/n0/mode/2up.: translated from the German by Phyllis Fox. This is an earlier version of the paper Courant, Friedrichs & Lewy 1967, circulated as a research report.
- Courant, R.; Friedrichs, K.; Lewy, H. (March 1967) [1928], "On the partial difference equations of mathematical physics", IBM Journal of Research and Development 11 (2): 215–234, MR0213764, Zbl 0145.40402, http://domino.research.ibm.com/tchjr/journalindex.nsf/a3807c5b4823c53f85256561006324be/769774a3c9f3685f85256bfa00683f8a!OpenDocument. A freely downlodable copy can be found here.
- Roberts, A. J. (2003), "A holistic finite difference approach models linear dynamics consistently", Mathematics of Computation 72: 247–262, doi:10.1090/S0025-5718-02-01448-5, MR1933820, Zbl 1008.37047, http://www.ams.org/mcom/2003-72-241/S0025-5718-02-01448-5.
External links
- Bakhvalov, N. S. (2001), "Courant–Friedrichs–Lewy condition", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c026760
- Weisstein, Eric W., "Courant-Friedrichs-Lewy Condition" from MathWorld.